Processus Décisionnels de Markov
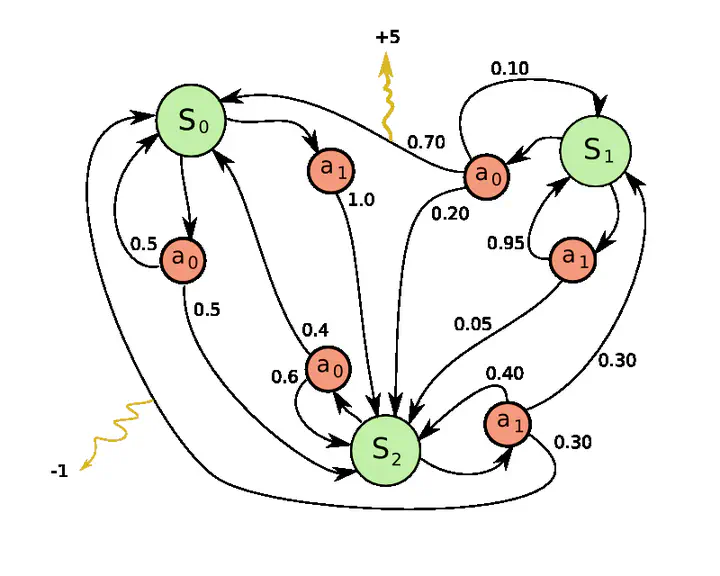 Exemple d’un MDP avec 3 états et 2 actions applicables par état
Exemple d’un MDP avec 3 états et 2 actions applicables par étatLa planification automatique est une branche de l’intelligence artificielle (IA) qui s’intéresse à trouver des plans (séquences d’actions) optimaux permettant d’atteindre un certain objectif. Dans certains problèmes, les actions ont des effets déterministes, tandis que dans d’autres, on ne peut pas être certain à l’avance de l’effet d’une action. Ce projet s’intéresse à ce deuxième cas, et plus précisément à l’étude des processus décisionnels de Markov. Les MDP sont aussi à la base d’une autre branche de l’IA nommée apprentissage par renforcement basé sur un modèle.
Dans les problèmes de planification probabilistes auxquels nous nous intéressons, il peut y avoir des millions, voire des milliards d’états à considérer. Vu les contraintes de temps souvent rigides (ex.: un robot extra planétaire qui doit prendre rapidement une décision sur sa prochaine action avant l’arrivée d’une tempête), la rapidité du temps de calcul d’une solution optimale d’un MDP est une caractéristique critique d’un bon planificateur. Or, les algorithmes de planifications classiques pour résoudre de tels problèmes, tels que Value Iteration (VI) et Policy Iteration (PI) ne sont pas assez rapides pour résoudre des problèmes ayant plusieurs millions d’états en un temps raisonnable.
Plusieurs algorithmes de planification ont été proposés dans la littérature pour diminuer le temps de calcul avant de trouver une solution optimale d’un MDP. Certains sont capables de concentrer les calculs sur des sous-régions prometteuses de l’espace d’états à l’aide d’algorithmes de recherche heuristique tels que LRTDP ou LAO* (les régions non-prometteuses sont élaguées ou peu considérées). Une autre catégorie d’algorithmes proposés utilisent des méthodes de partitionnement pour décomposer l’espace d’états en sous-régions. Le but étant de diminuer les calculs inutiles qui font propager les valeurs d’états à travers des cycles, et de permettre de résoudre plusieurs régions en parallèle. Les algorithmes P3VI et TVI font parties de cette catégorie d’algorithmes.
Une façon orthogonale d’accélérer les calculs est de considérer comment les algorithmes de planification sont implémentées. Dans ce projet, nous considérons des éléments d’architecture tels que la hiérarchie de mémoire ainsi que les différents niveaux de parallélisme des ordinateurs modernes dans le contexte des algorithmes de planification pour MDP. Nous proposons une nouvelle structure de données pour représenter les MDP en mémoire, que nous appelons CSR-MDP (pour compressed-sparse-row-MDP). Cette structure de données a l’avantage de compacter tout le MDP en mémoire et d’ainsi diminuer/accélérer les accès mémoire et ce, peu importe l’algorithme de planification utilisé. Nous proposons aussi une version parallèle de l’algorithme TVI, que nous appelons pcTVI (pour parallel-chained TVI).
Dans ce projet, nous avons développé une librairie C++ de planification de SSP-MDP qui supporte des algorithmes classiques tels que VI, LRTDP et TVI, de même que les nouveaux algorithmes proposés (pcTVI, eTVI, eiTVI) utilisant notre nouvelle représentation mémoire, CSR-MDP.